Central to our comprehension of time is the intricate interplay between the celestial dance of heavenly bodies and the pursuit of accuracy. Throughout history, mankind’s perception and quantification of time has evolved with its interaction with the natural environment.

From ancient times when the rhythm of the Sun governed daily existence to the modern day of standardised timekeeping ushered in by mechanical innovations, human ingenuity has been instrumental in shaping this odyssey. Unfolding within this tale is the rare horological complication, the equation of time, a captivating chapter in the ongoing saga of humanity’s temporal exploration.

The Audemars Piguet Jules Audemars, an equation of time watch from the era of modern timekeeping

Dawn of Timekeeping: Celestial Observations and Ancient Innovations

The genesis of civilisation ushered in humanity’s bond with the cosmos, as early communities devotedly charted the celestial events that dictated the rhythm of their lives. This connection was not merely academic; the alternation of day and night, the moon’s phases, and the Sun’s shifting journey through the heavens were the foundation upon which the ancients built their methods of marking time.

In civilisations like those of Mesopotamia, Egypt, and ancient China, a deep-seated knowledge of the heavens was crucial for survival. The predictable cycles of day and night governed the timing of essential activities such as hunting and gathering. At the same time, the moon’s waxing and waning phases were indispensable guides for agricultural practices.

These societies were pioneers in the science of timekeeping, centring their systems around the concept of “true” solar time, with the Sun’s path as the ultimate timekeeper. The sundial, a quintessential example of early-time measurement devices, showcased this solar dependence, facilitating the division of the day into quantifiable parts. In 1500 BC, the Egyptians advanced this concept by splitting the day into 24 segments, a revolutionary step despite the fluctuating length of the day with the seasons and geography.

An Egyptian “shadow” clock from the Ptolemaic period (306–30 B.C.E.). Image – Metropolitan Museum of Art

Going even further back to 2000 BC, the Babylonians devised a sophisticated base-60 numerical system. Their contributions to time division were monumental, paving the way for the modern understanding of hours, minutes, and seconds. This comprehensive segmentation of the day marked a critical leap forward in the human capacity to grasp and manage time, fostering the development of more complex timekeeping instruments across subsequent generations.

The quest for more precise timekeeping can be traced back to Claudius Ptolemy in the second century AD. In his Almagest, the Alexandrian mathematician, astronomer, astrologer and geographer addressed the Sun’s elliptical orbit and its varying speeds, setting the stage for future time measurement corrections. His insights laid foundational knowledge that would ultimately guide advancements in timekeeping accuracy.

Aligning Shadows: The Evolution of Sundials and the Quest for Equinoctial Hours

In the 13th century, Islamic mathematicians and astronomers achieved a landmark advancement in time measurement by enhancing the accuracy of sundials. They innovated by adjusting the sundial’s gnomon to align parallel with the Earth’s axis, enabling it to consistently measure hours of equal length throughout the year, regardless of the season.

This innovation led to the creation of the apparent solar day, the time between consecutive solar transits at a given location, which varies throughout the year but is approximately 24 hours. The mean solar day, on the other hand, is made up of equinoctial hours – 24 hours of equal length.

A horizontal sundial with a qibla indicator and compass made by Bayram Ibn Ilyas dating from 1582-83. Image – British Museum

The profound understanding of the connection between celestial dynamics and timekeeping manifests itself in the ancient design of Analemma sundials. The pioneering works of astronomers like Tycho Brahe (1546-1601) and Johannes Kepler (1571-1630) further highlight it.

Kepler’s significant contributions, in particular, were applied by the Flemish astronomer Johannes Stadius, or Estadius, (1527-1579) in an ephemeris published around 1570. This work contained a detailed table known as the Canon aequationis dierum naturalium ex Copernici doctrina, or “Canon of the equation of natural days from Copernicus’s doctrine,” showcasing the ongoing endeavour to bridge the gap between solar time and mean time.

Jost Bürgi: Bridging Seconds and Celestial Cycles in the Dawn of Precision Timekeeping

In 1584, Jost Bürgi (1552-1632), a Swiss clockmaker, astronomer, and mathematician employed at the observatory of William IV, Margrave of Hesse-Kassel, unveiled a groundbreaking creation: the world’s first observation clock capable of measuring time to the second.

This innovation marked a revolution in timekeeping accuracy, facilitating the inaugural star survey using the horizontal method and slashing the daily error margin of clocks from a substantial quarter-hour to just one minute—an unprecedented improvement for the time, but for many years, unfortunately, unique to Bürgi’s work.

Jost Bürgi. Image – Wikimedia Commons

The cornerstone of Bürgi’s success was his introduction of the cross-beat escapement and a weight-driven remontoire, coupled with his precision in gear crafting. These innovations enabled the tracking of seconds visually and audibly, significantly enhancing the accuracy of astronomical observations.

Among his remarkable achievements is the Vienna Crystal Globe Clock, an exquisite timepiece Bürgi produced in his Prague workshop. Commissioned by the Prince of Liechtenstein for Emperor Ferdinand II, this clock is a testament to Bürgi’s legacy in marrying fine craftsmanship with precision timekeeping. His work, including an astronomical clock commissioned by William IV in 1591, exemplifies the fusion of science and art, featuring technological novelty and aesthetic elegance.

The Viennese Crystal Clock made by Jost Bürgi. Image – Kunsthistorisches Museum.

The historical discourse on Bürgi’s clocks often delves into their classification as the first “equation” clocks, acknowledging Bürgi’s role in introducing this concept. While debate exists over whether his clocks were more aligned with lunar than solar equations, Bürgi’s collaborations with Tycho Brahe and Johannes Kepler and his inclusion of mechanisms to measure true solar time underscore his significant contributions to solar equations.

But before the advent of the pendulum clock, Bürgi encountered significant challenges in synchronising meantime with solar time, partly due to the absence of precise tables and the mechanical limitations of his era. Despite these hurdles, Bürgi’s innovations laid crucial groundwork for future timekeeping advancements.

Solar Time and Mean Time: An Evolution in Timekeeping

The fluctuations in the length of solar days throughout the year stem from two key astronomical factors: the Earth’s axial tilt and its elliptical orbit around the Sun. Johannes Kepler’s seminal work on the Laws of Planetary Motion, particularly his first two laws published in 1609 in Astronomia Nova, revolutionised our understanding of the solar system. Kepler showed that planets travel in elliptical orbits with the Sun at one focus, not in perfect circles as previously thought. This fundamental shift in understanding was a crucial advancement in astronomy and significantly impacted timekeeping and navigation.

Despite their inherent inaccuracies, even the earliest mechanical clocks were designed to follow the Sun’s cycle. Consequently, communities faced the perpetual task of tweaking their public and personal timepieces to synchronise with the irregular length of solar days. Yet, with advancements in clockmaking technology, the constraints of strictly adhering to solar time became evident. This impracticality prompted the quest for a more dependable method of timekeeping, with “mean time” emerging as a solution.

An engraving of Johannes Kepler by N. Dietz. Image – Wikimedia Commons

The comprehension of time measurement using the Sun’s position and establishing a standardised timekeeping system to counter the Sun’s irregular movement illustrates the transition from Solar Time to Mean Time. Solar Time, reliant on the Sun’s peak position between consecutive solar noons, experiences variability, prompting the widespread acceptance of Mean Time, which normalises a day’s duration to precisely twenty-four hours.

Central to Mean Time are the conceptual models of the Mean Sun and the Dynamical Mean Sun. These idealise the Sun’s motion as if it traversed the sky uniformly, a solution ingeniously designed to counterbalance the actual Sun’s apparent erratic path. This system ensures that our timekeeping methods remain synchronised with the cosmic cycle. Establishing the benchmark, the Mean Sun figuratively traverses the Greenwich meridian precisely at 12:00 pm GMT on the Vernal Equinox, acting as a distinct temporal landmark.

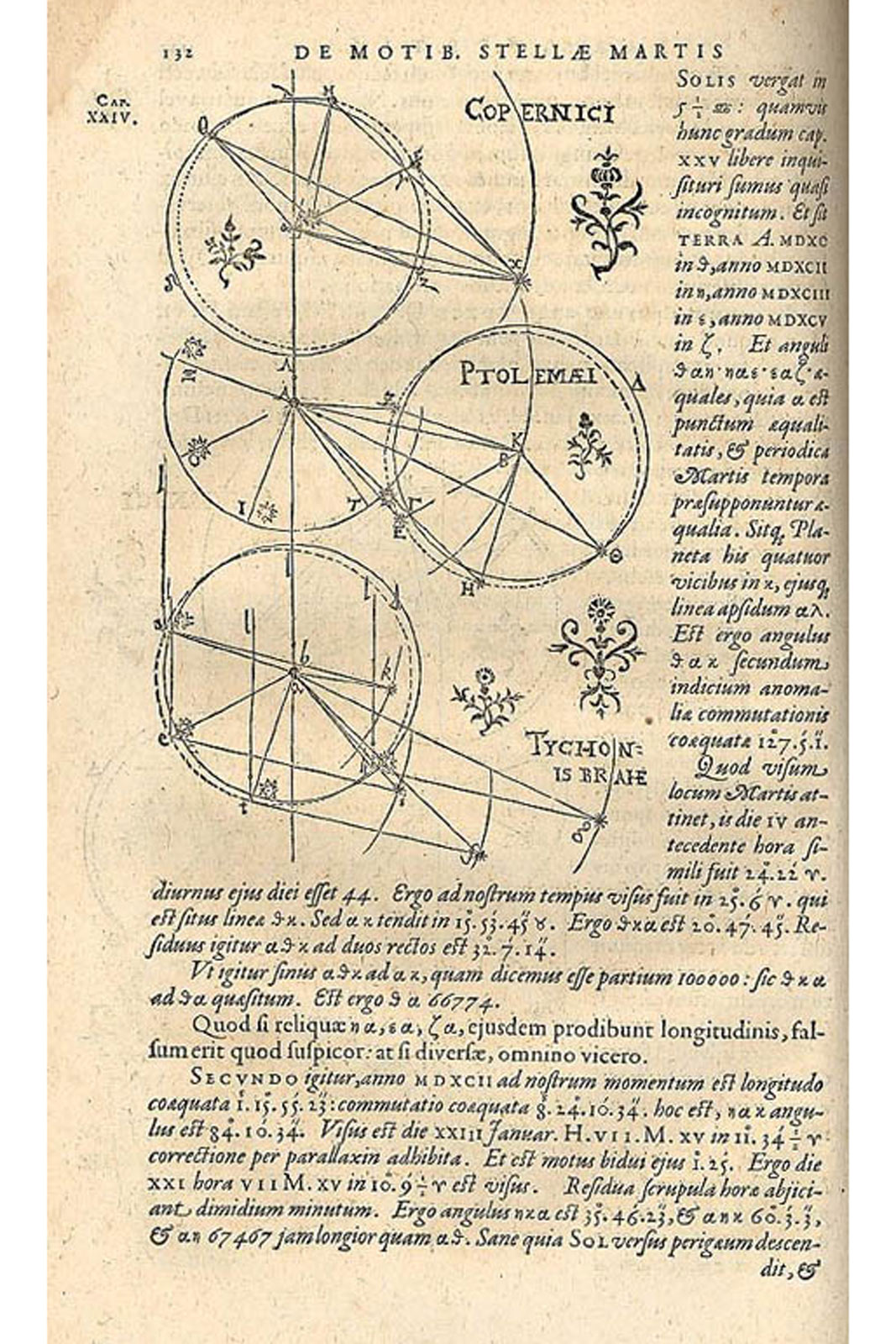
Diagrams of the three models of planetary motion as mentioned in Kepler’s Astronomia Nova published in 1609. Image – Wikimedia Commons

Huygens Pendulum: Bridging Timekeeping and the Cosmos

As communities expanded and the intricacies of trade, governance, and navigation grew more complex, the mid-17th-century introduction of precise mechanical clocks engineered for consistency precipitated the shift towards mean solar time.

In 1656 Christiaan Huygens postulated that an oscillator makes for a good timekeeping base, thus presenting the world with the pendulum clock. A mathematician, Huygens recognised that a free gravity pendulum is not intrinsically isochronous and invented the so called “cycloidal pendulum”. His pendulum would feature a flexible string  weighted at one end, with the string coming in contact with cycloidal flanks which would shorten the pendulum’s length for large amplitudes. 

In 1657, with the help of clockmaker Salmon Coster, Huygens turned his concept into a prototype timekeeper which was said to run at a daily deviation of only 15 seconds per day . In practice the specialised cycloidal pendulum proved not all that reliable and was mostly abandoned in favour of large pendulums oscillating at small amplitudes. 

The validity of Huygens’ cycloidal pendulum can be verified today by differential calculus, which makes his discovery all the more impressing, since differentials were invented by Sir Isaac Newton only some 30 years later. Huygens only used graphical reasoning and geometry in building his curve theories, which still stand today. 

Portrait by Christiaan Huygens made by Caspar Netscher in 1671. Image – Kunstmuseum Den Haag

What Huygens did for horology cannot be understated. He introduced true oscillating systems as timebases — compared to the previous inertial-only foliots, and summed up his findings in the seminal work Horologium Oscillatorium (1673). In the same volume he also wrote about the resonance principle and various escapements.

Huygens was probably the first to take a rigorous mathematical approach to watchmaking. If before him watchmaking was mostly an artisan craft, his findings turned horology into a proper science. He later went on to invent the modern hairspring-balance assembly (invention disputed by the English Rober Hooke, who claimed priority).

Huygens’ inventions laid the foundation for future advancements in horology, paving the way for more sophisticated timekeeping mechanisms and techniques. His pioneering work, both theoretical and practical, underscored the profound impact of mechanical precision on our comprehension and organisation of time, shaping the trajectory of timekeeping science for centuries to come.

A pendulum clock built by Dutch clockmaker Salomon Coster from 1657 (left) next to a copy of Huygens’s Horologium Oscillatorium published in 1653 (right) as displayed in the Museum Boerhaave, Leiden. Image – Wikimedia Commons

Equation Tables: Revolutionising Timekeeping

The advent of Huygens’ pendulum clock in precision timekeeping heralded a significant breakthrough. It laid the groundwork for developing more accurate equation tables, a crucial tool for reconciling solar and mean time.

As already understood, the length of a solar day is not constant. It fluctuates throughout the year, leading to time differences ranging from +14 minutes and 16 seconds to -16 minutes and 24 seconds. These differences are particularly noticeable on specific days, such as February 11th and November 3rd.

In 1665, Huygens introduced groundbreaking tables leveraging the precision of the pendulum to elaborate on the equation of time. By integrating this innovative technology, Huygens effectively bridged the divide between human-made timekeeping systems and the natural cadences of celestial bodies.

Thanks to the unparalleled precision of the pendulum clock, these tables quickly became indispensable for a more dependable and precise approach to timekeeping, effectively aligning mechanical timekeeping with the natural progression of days.

Equation Tables published by Robert Sayer, London. Image – Tobias Birch Clocks

Expanding on Huygens’ pioneering work, the astronomer royal John Flamsteed (1649-1719) released enhanced tables in 1672 and 1673, providing vital corrections and refinements. These tables underwent continuous improvement and standardisation efforts, reflecting a concerted push to elevate the accuracy and reliability of timekeeping instruments.

This innovation set the stage for creating clocks capable of directly displaying the equation of time. Its impact extended beyond history and astronomy, proving invaluable in practical areas such as navigation.

Deriving from the medieval Latin phrase aequātiō diērum, meaning “equation of days,” the concept of the equation of time (EoT) emerged as a crucial mathematical tool in timekeeping.

Aligning Sun and Clock: Innovations in Manual Time Correction Methods

In the latter part of the 17th century, the refinement of equation tables led to the creation of timekeepers that allowed for manual adjustments for the Equation of Time. Integrating the Sun’s equations into clock mechanisms was realised through four primary methods, each offering a unique approach to aligning mechanical time with solar time.

The first and most straightforward method involved using a sundial alongside a regulator clock. This approach allowed for a basic comparison between solar time, as indicated by the sundial, and meantime, as kept by the clock, necessitating manual adjustments to reconcile the two.

The second method employed an analemma, a figure-eight curve that graphically represents the Sun’s apparent movement over a year. By marking a specific point on the analemma, clocks could visually display solar time and approximate the necessary corrections for the EoT, offering a visual guide for adjustment.

Analemma depicted on a globe. Image – Wikimedia Commons

A more interactive third method required frequent manual adjustments of a clock’s dial based on equation tables. This method could involve various modifications, such as using minute hands divided into segments or an adjustable minute ring to reflect the day-to-day changes in the EoT accurately. This hands-on approach allowed clock users to directly apply the corrections, making the timepiece as accurate as possible.

The fourth and most complex method involved creating clocks with a full-year calendar mechanism. This mechanism forgoed traditional zodiac signs in favour of a calendar that presented the equations in a tabular format. This more sophisticated system aimed to provide a comprehensive overview of the corrections needed throughout the year, albeit at a higher cost and complexity.

Notably, none of these methods offered an “automatic correction” for the EoT; instead, they necessitated either direct manual adjustment or extrapolation based on equation tables. This reliance on manual intervention highlighted the ongoing challenge of achieving a seamless integration of solar and meantime, underscoring the technical limitations of the era’s timekeeping solutions.

Nicholas Mercator and the Advent of EoT Clocks

As seen previously, the introduction of the pendulum clock represented a leap in accuracy. It set the stage for a more profound reconciliation of the fundamental differences between solar and mean time, underscoring the continual quest for precision in measuring time.

In 1666, Nicholas Mercator (1620-1687), a mathematician distinct from the renowned cartographer Gerardus Mercator, contributed to developing EoT timekeepers. John Evelyn, a diarist and founding Fellow of the Royal Society, documented his efforts. Mercator’s innovative clock, unveiled at Gresham College, caught the attention of the Royal Society, capturing the interest of figures like Sir Robert Moray and Dudley Palmer, both Fellows of the scientific institution.

An entry from Evelyn’s diary on August 29th, 1666, highlights the moment Mercator showcased his invention. At the time, an antiquary and natural philosopher, John Aubrey, noted the clock’s substantial size at “a foot across,” hinting at its complexity and the formidable challenges it posed to even skilled clockmakers like Joseph Knibb (1640-1711).

Designed “to perform the equation,” Mercator’s clock was engineered to correct the equation of time, thereby synchronising solar and mean time. The lack of comprehensive records or evidence of widespread usage leads to speculation regarding the functionality and popularity of the device. Although detailed mechanics of Mercator’s equation clock are not fully documented, theories suggest it might have featured a pendulum capable of automatically correcting for the equation of time. Mercator’s induction into the Royal Society on November 14th, 1666, is a testament to his significant contributions to the horology field.

An excerpt from John Evelyn’s diary entry for August 28, 1666. Image – Internet Archives

Furthermore, Nicholas Mercator’s collaboration with Ahasuerus Fromanteel (1607-1693), a distinguished clockmaker from London and a protégé of Salomon Coster—who had crafted the initial pendulum clock prototype for Christiaan Huygens—symbolised a significant effort to blend mathematical breakthroughs with the art of clockmaking.

Mercator’s pioneering initiatives seem to have paved the way for future advancements by a cadre of English scientists and clockmakers, including Robert Hooke (1635-1703), Thomas Tompion (1639-1713), Daniel Quare (1649-1724), and George Graham (1673-1751), who pursued further innovations in equation clocks.

Shaping Time: The Genesis of the Equation Cam

In the late 17th century, London’s clockmaking landscape experienced a remarkable surge of innovation and collaboration, fuelled by interactions among prominent horologists and the broader scientific community. Among this period’s leading figures were Christian Huygens and Robert Hooke, who made substantial strides in crafting clocks that could precisely display solar time without the need for cumbersome equation tables.

This era marked the advent of the equation cam, a revolutionary mechanism designed to reconcile the disparities between solar time and mean time. Inspired by the analemma—a figure-eight pattern illustrating the Sun’s varying positions in the sky throughout the seasons—these mechanisms featured a distinctive mathematically calculated kidney-shaped cam, symbolising a pivotal step forward in horological precision and accuracy.

At the heart of this innovation lies the cam and lever mechanism, an integral component of the invention. It comprises a shaft propelled by the clock’s mechanism, completing a full rotation annually. Affixed to this shaft is a meticulously crafted kidney-shaped cam, tailored precisely to match the annual fluctuations outlined by the equation. This cam engages with a follower and a connected lever, facilitating the seamless translation of its rotational motion into practical adjustments within the timepiece.

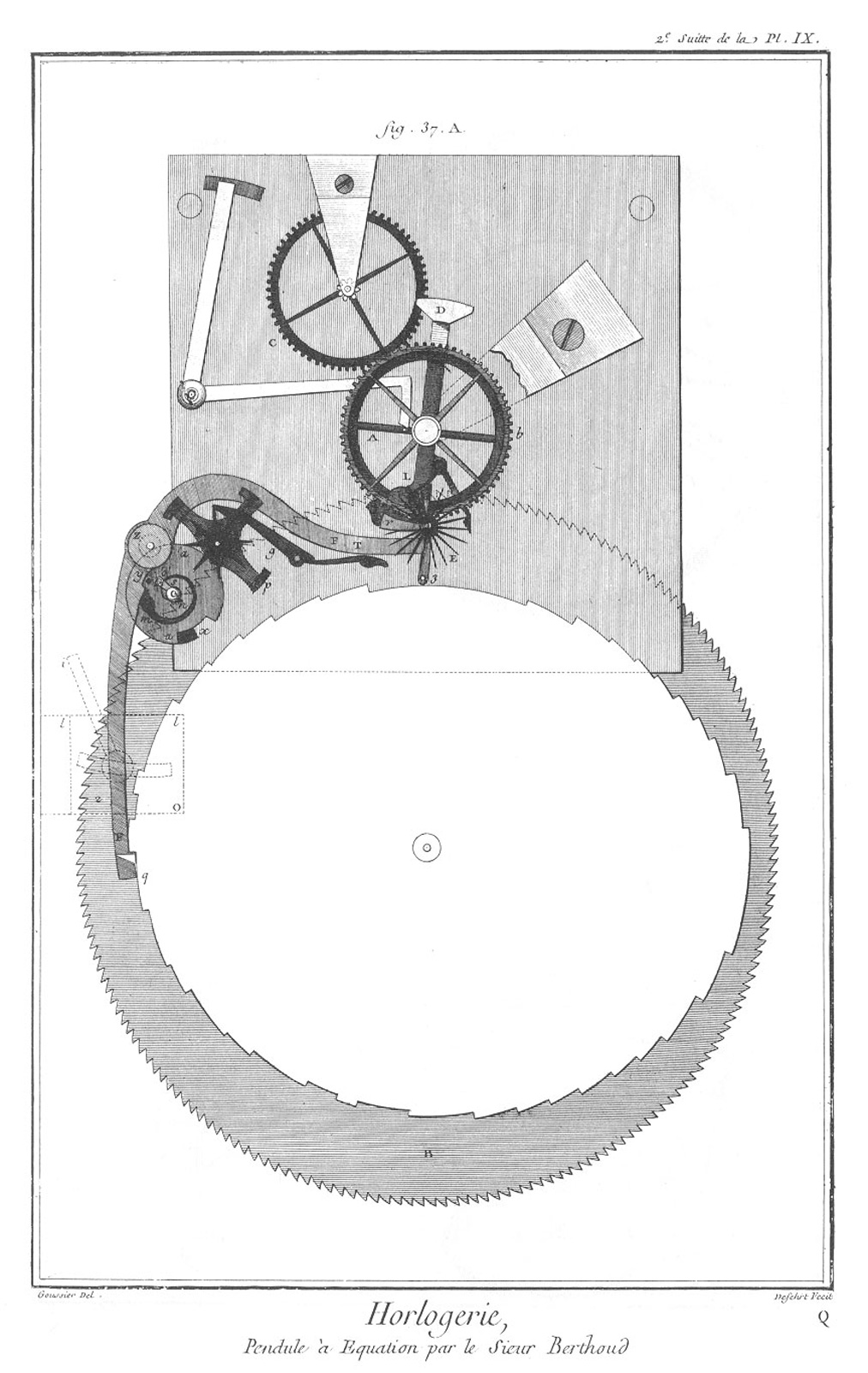
Drawing of an equation pendulum by Ferdinand Berthoud (1727-1807). Image – Encyclopédie de Diderot et d´Alembert

As the cam rotates throughout the year, the follower meticulously follows its evolving contour, adjusting to its dynamic profile. This precise interaction effectively translates the cam’s slow motion into direct, understandable adjustments. Such a mechanism guarantees that the clock faithfully reflects the shifts between solar and mean time across the year, adeptly capturing both the advancements and the delays in solar time in comparison to meantime.

The date indication feature plays a crucial role in this mechanism, ensuring the cam rotates at the appropriate pace all year round. It also facilitates daily precision adjustments according to the current date, reinforcing the timepiece’s function as a reliable indicator of solar time.

Christiaan Huygens contributed to the development of solar time indication, hinting that the concept of the equation clock was already known among clockmakers. By 1695, he would be credited with devising a nephroid-shaped equation kidney mechanism. Unfortunately, the specific equation clock that featured this innovation, intended for the University of Leiden, has since been lost to history.

Portrait of Robert Hooke as depicted by Rita Greer.

Robert Hooke, known for his deep interest in horology and his significant partnership with Thomas Tompion, may also have contributed to the development of equation clocks. Tompion’s creations, frequently inscribed with “Tho. Tompion Invenit,” indicate a collaborative effort with Hooke that can significantly have contributed to refining the equation clock mechanism.

Joseph Williamson (1673-1725), an Irish clockmaker who moved to London, further contributed to this field. Trained in Dublin, Williamson gained recognition by the 1690s and collaborated with Daniel Quare to produce sophisticated longcase clocks with EoT indication. Despite claims in a letter to the Royal Society about crafting all equation movements sold in England before 1720, verifying his contributions still needs to be determined due to the loss of historical pieces, such as the clock made for King Charles II of Spain.

The invention and refinement of the equation clock underscore a period rich in innovation. Despite the speculative nature surrounding their claims, the contributions of Huygens, Hooke, Tompion, Quare, and Williamson highlight a shared pursuit of precision in timekeeping. While unresolved, the debate over the origins of the kidney cam clocks reflects the complexity of scientific communication and, to a certain level, the collaborative spirit that drove horological advancements in the 17th and 18th centuries.

Tompion fecit: Equation clocks with movable minute markings

Equation clocks with movable minute markings represented the next step, enabled by the innovative use of the equation cam. These precision instruments featured a minute plate that could rotate independently around the clock’s axis, a design that accurately mirrored the EoT, eliminating the need for manual adjustments and aligning perfectly with solar time.

Thomas Tompion, a distinguished English clockmaker and the son of a Bedfordshire blacksmith, established his reputation in the field upon setting up his workshop near Fleet Street in 1671. His collaboration with the mathematician and scientist Robert Hooke significantly contributed to his fame.

An engraving of Thomas Tompion by John Smith. Image – Yale Museum of Art

Tompion’s 1695 equation timepiece for King William III, now a prized item in Buckingham Palace, exemplifies his horological mastery. This clock introduced a way to display the EoT directly on its face, with the hour hand completing a full rotation every 24 hours, eliminating the need for an additional hour-equating ring.

A floor standing clock made by Thomas Tompion from 1695. Image – The Royal Collection Trust

The Equation Kidney mechanism, pivotal to the mechanism’s design, is cleverly mounted alongside the annual calendar disc. It employs a pin attached to a lever, which, depending on its position, moves a minute ring forward or backward to adjust for the EoT, showcasing Tompion’s inventive engineering.

Among Tompion’s notable creations is the Drayton House Year Equation longcase clock, made between 1696 and 1700. Intended initially for Drayton House, it became part of the Duchess of Norfolk’s estate, reflecting its artistic value and the turbulent history of its ownership. This clock features a unique design with a silvered chapter ring and a rotating minute ring for dynamic time measurement, underscoring Tompion’s signature innovation.

The Drayton House Clock made by Thomas Tompion for the Duchess of Norfolk. Image – The Fitzwilliam Museum, Cambridge

Tompion’s collaboration with his nephew Edward Banger (1668-1720) from 1699 to 1704 resulted in another remarkable timepiece with movable minute markings. Their joint effort produced a clock with advanced features like a dual representation of apparent and mean time and a sophisticated calendar mechanism that accounted for leap years.

Commissioned for Prince George of Denmark and later chosen by George III for Buckingham House, this clock is recognised for its exceptional craftsmanship and intricate design. It survived historical challenges like the 1809 fire at St. James’s Palace.

17th to 18th century: Blending Timekeeping with Celestial Wonder

The transition from the rudimentary practice of aligning timekeeping with solar time through sundials and the EoT tables to integrating complex astronomical features in clocks mirrors a significant evolution in horology and societal engagement with the cosmos. As the 17th century drew to a close, despite the advancements in clockmaking exemplified by figures like Thomas Tompion, setting clocks to mean time remained cumbersome, tethered to the direct observation of sundials and subsequent adjustments using EoT tables. While practical, this method underscored contemporary timekeeping’s limitations in accurately capturing the nuances of celestial mechanics.

Recognising the inconvenience and inaccuracy of perpetual reliance on EoT tables, clockmakers in the early 18th century began exploring more sophisticated solutions. This period witnessed a renewed interest in clocks that served as timekeeping instruments and conduits for astronomical education and display. With their elaborate dial indications, these timepieces offered their owners a platform to showcase their understanding and appreciation of the universe. This trend was not merely a reflection of technological progress but also an expression of the era’s intellectual curiosity and the social prestige associated with astronomical knowledge.

An engraving of the astronomical clock at the Strasbourg Cathedral by Tobias Stimmer, 1574. Image – The Metropolitan Museum of Art

The phenomenon of creating clocks with intricate celestial displays harks back to the medieval era, when monumental public clocks, such as those in Strasbourg Cathedral and the Old Town Square in Prague, were designed to illustrate the marvels of the divine cosmos to the masses. This tradition of blending clockmaking with astronomical display continued into the Renaissance, finding expression in the princely courts of Europe, such as the Viennese’ Kunstkammer. Here, grand astronomical clocks crafted by luminaries like Eberhard Baldewein (1525-1593) and Jost Bürgi were not just mechanisms for marking time but statements of power, knowledge, and the cosmic order.

The 18th century’s resurgence in astronomical clockmaking thus can be seen as part of a long historical continuum, where the mechanics of timekeeping converge with the aesthetics of cosmic representation. These clocks, far from mere technical achievements, were symbols of their owners’ erudition and the broader human quest to understand and articulate our place within the universe. Through the intricate dance of gears and hands, they narrated the story of humanity’s timeless fascination with the stars and the ceaseless pursuit of precision in our temporal and celestial comprehension.

Tracing the Arc of Time: The Innovation of Variable Pendulum Clocks

The dawn of the 18th century saw the introduction of variable pendulum clocks, designed to accurately mimic the annual variations of solar time. These clocks featured an ingenious mechanism to adjust the pendulum’s length, altering its oscillation speed to match the Earth’s irregular rotation. This technological marvel directly reflected solar time, eliminating the need for cumbersome conversions typically associated with equation tables.

As noted by Joseph Williamson, these clocks incorporated a directly actuated equation kidney that influenced the pendulum’s suspension. This permitted an alteration in pendulum length, facilitating a direct readout of apparent solar time with a singular set of hands. Remarkably, some of these timepieces were designed to toggle between mean and apparent time displays, demonstrating their versatility to accommodate varying timekeeping needs. An exemplary model of this innovation is the year clock by Quare, housed at Hampton Court and later refined by Benjamin Vulliamy (1747-1811), reflecting the dynamic evolution of these sophisticated mechanisms. Williamson’s inventive approach considered the strategic up-and-down movement of the suspension spring through a slit.

A floor standing clock made by Daniel Quare for King William III. Image – The Royal Collection Trust

The Encyclopédie by Diderot and d’Alembert further illuminated this subject, introducing Father Alexandre’s (1705-1772) design that also utilised an elliptical lever to adjust the pendulum length according to the solar year’s requirements. This approach elegantly bridged theoretical physics and practical mechanics, although adapting the design to accommodate heavier pendulums posed considerable challenges.

Visualising the Equation: Introduction of Subsidiary Dials

Beginning in 1767, the Nautical Almanac and Astronomical Ephemeris published by the Royal Greenwich Observatory introduced tables for the equation of time, broadly guiding users to adjust apparent time by a simplified method that required adding or subtracting indicated minutes and seconds to obtain meantime.

Representing the third phase in the evolution of timekeeping mechanisms accommodating the EoT, these systems employed a “Wand” or rocking hand moving across a fixed semicircular dial or arc. This approach, from -16 to +14 minutes, visually represented the Equation of Time, enabling users to discern the difference between mean and true solar time easily. However, this method still necessitated mental calculations for accurately converting mean solar time to true solar time.

Early astronomical and equation clock dial by Jack Willmore (1674-1720) and A. Malines from circa 1711. Image – Sothebys

This wave of innovation underscored a dedication to creating a more intuitive and accessible means for the public to grasp the EoT. By incorporating visual indicators that illustrated the mathematical variance between solar time and mean time, clockmakers made it significantly more user-friendly.

Prominent figures in this movement include Daniel Quare, who was credited with producing five notable examples, the earliest of which dates between 1690 and 1700, as documented by the British Museum. Edward Cockey, Thomas Tompion, Jack Willmore and John Ellicott (1706-1772) also stand out for their contributions to this sophisticated blend of artistry and science. Their work collectively marks a significant period of advancement and creativity, bridging complex astronomical phenomena with the everyday act of timekeeping.

Detail of the dial of the astronomical longcase clock made by Edward Cockey (died 1768). Image – British Museum

Mechanical Mastery: Advent of Built-in Equation Calculations

The next step introduced further developments in a sophisticated system capable of adjusting rotational speeds. This solution underscored early clockmakers’ profound understanding of mechanics by enabling clocks to synchronise and automatically exhibit solar and mean time.

Featuring a sophisticated arrangement of interlocking gears, this system transmitted rotational motion from various sources to a single output, ensuring the seamless integration of different time measurements within a single timepiece. Through synchronising hour and minute hands with the variable speed driven by the EoT cam, a differential gear facilitated its direct indication on the clock face.

This elaborate system achieved remarkable accuracy by harmonising the constant rotation of the meantime gear with the fluctuating rotation controlled by the EoT cam, accurately representing true solar time. Typically highlighted on the clock face by a distinct hand or sub-dial, this significantly elevated the complexity and functionality of the timepiece.

Obverse of the Antikythera mechanism found in 1901 and on display at the National Archaeological Museum, Athens. Image – Wikimedia Commons

The historical journey of epicyclic and differential gears is deeply intertwined with advancements in watchmaking and mechanical engineering. These gears have proven indispensable, from their crucial role in depicting the EoT in timekeeping devices to their extensive application in modern machinery, computing, and control systems. Notably, the innovation at the heart of this dual-time display has predated its modern application for centuries.

The discovery of the Antikythera mechanism in 1901, recovered from the depths of the Greek Mediterranean, revealed an ancient artefact dating back to 100 BC to 70 BC. This device, a testament to ancient mechanical prowess, evidences one of the earliest forays into complex mechanical engineering.

Reverse of the Antikythera mechanism found in 1901 and on display at the National Archaeological Museum, Athens. Image – Wikimedia Commons

Modern analysis suggests that the Antikythera mechanism utilised a system similar to differential gearing to calculate lunar phases by determining the angular difference between the Sun and Moon’s positions on the ecliptic. This early use of differential gearing highlights a sophisticated understanding of mechanical operations and showcases the advanced technological capabilities of ancient civilisations.

The resurgence of this mechanism in 1575 with Baldewein’s globe clock marked a revival in its application. It proliferated during the Renaissance through the advent of astronomical clocks in South Germany and Austria, marking a significant advancement in horological science.

A celestial globe clock made by Eberhard Baldewein from 1574. Image – Kugel Collection, Paris

By the 18th century, horologists such as Tompion, Graham, and Joseph Williamson had refined the differential gear, laying the groundwork for its later use in industrial machinery.

Williamson Double-Dialled EoT clock

A singular category in this type of time indication comprises clocks and watches featuring dual displays or double dials. These timepieces simultaneously display mean and solar time through separate hands and dials, allowing observers to view the current time according to the conventional mean and natural solar time.

An example of such a timepiece emerged around 1720, made by Joseph Williamson, just a few years before his passing in 1725. Unlike earlier examples, this timepiece featured separate dials for mean and apparent time, both driven by a single movement housed between them.

The clock’s subsidiary dials were arranged in a unique configuration. One dial displayed the days of the week, each symbolised by intricately engraved representations of their corresponding deities. Another dial indicated the age of the moon and high tide times, allowing for practical maritime use.

A double dialed clock with an equation of time made by John Williamson from 1720. Image – British Museum

At the heart of the clock lay the equation dial, where the equation kidney, responsible for adjusting the clock to display apparent solar time, was driven by an endless worm gearing mechanism allowing for precise synchronisation between mean and apparent time.

A clever feature of the clock was the ability to switch between mean and apparent time displays. By manipulating a knob located near the winding drum, the roller on the equation dial could be disengaged, allowing mean time to be shown on both dials simultaneously.

Additional features, such as a disc indicating the approximate rising and setting of the Sun and a revolving blued steel band tracking the Sun’s daily position in the heavens, added to the clock’s functionality.

The clock’s engineering brilliance is evident in its construction. Both sets of hands are driven by a single driving train, simplifying the mechanism while ensuring smooth and accurate timekeeping. Additionally, a second disc attached to the arbour carrying the calendar hand and equation kidney facilitates the rotation of the Sun’s motion plate, providing essential astronomical information.

1750 to 1850: the Golden Era

The period from 1750 to 1850 was indeed a golden era for advancing horology, particularly in the refinement and application of the EoT in timekeeping devices. This period saw a remarkable transition in measuring and displaying time, reflecting the era’s broader scientific understanding and technological capability shifts.

In post-1755 England, the production of equation clocks saw a decline. This shift may reflect changing tastes, technological advancements, or the practical considerations of manufacturing and maintaining such complex devices. Despite this, the fascination with and the craft of creating equation clocks persisted more robustly among French horologists, indicating a divergence in horological traditions between the two countries.

French makers like Ferdinand Berthoud and the Lepaute brothers (Jean-André 1720-1789 and Jean-Baptiste 1727-1802), alongside others such as Robert Robin (1741-1799) and Charles Oudin (1768-1840), continued to innovate, developing clocks and watches that not only were masterpieces of mechanical complexity but also served as luxury items and symbols of scientific progress.

A longcase astronomical regulator clock made by Ferdinand Berthoud dating from circa 1768 to 1770. Image – Metropolitan Museum of Art

This divergence underscores the unique cultural and scientific contexts in which these horologists worked. In France, the continued popularity and production of equation clocks may have been driven by patronage, the prestige of scientific instruments, and a national interest in astronomy and navigation. Meanwhile, British horological interests shifted towards the practical and commercial aspects of timekeeping, as seen in the emphasis on marine chronometry and the quest for determining longitude at sea.

The period’s legacy in horology is not just in the advancements made but in the enduring fascination with the equation of time and the relentless pursuit of precision. It was a time when the artistic and the scientific were intricately linked in the craft of timekeeping, leading to innovations that would lay the groundwork for future developments in the field.Overall, this era’s significance in horological history cannot be overstated. It was a period of refinement and revolution, where the challenges of accurately measuring and displaying time spurred remarkable innovations.

Rise of the “Equation Marchante”

“In principle, the indication of true solar time with a mean time clock is simple enough. It is necessary only to arrange a suitably shaped cam to revolve once a year and a pivoted hand to indicate the equation for the day by its rise and height on the cam. The indication of the equation as a relative interval of time between two continuously revolving hands is more complicated.”

– George Daniels, The Art of Breguet (1975)

The “running equation” mechanism, also known as équation marchante, represents the last step in the historical and technical evolution of displaying the EoT. It offers users a more intuitive experience, allowing for direct readings of solar time without manual adjustments due to its automatical compensating capability.

As seen in Williamson’s double-dialled clock, the mechanism uses a feeler lever to interact with a differential system, controlling the position of the Equation hand relative to the minute hand. As both hands progress around the dial simultaneously, users can quickly identify true solar noon when the Equation hand aligns with noon.

An astronomical stop-watch with equation of time by John Ellicott (1706-1772) in collaboration with Thomas Mudge (1715-1794), London, circa 1742. Image – Antiquorum

At the core of this system lies the already discussed differential gear capable of combining two inputs into one output. One input represents the constant rotation reflecting mean solar time, while the other adjusts for the variable EoT.

This sophisticated setup features two coaxially positioned minute hands: one dedicated to precisely tracking mean solar time, and the other—the EoT hand—dynamically adjusts to reflect true solar time variations. This way, users gain a deeper understanding of temporal variations by observing the real-time fluctuation between solar and conventional clock time.

Despite its complexity, reading the indication on the dial is surprisingly straightforward. A hand, often crafted in gold as a nod to tradition and adorned with a small sun, moves alongside the conventional minute hand but at a variable speed dictated by the Earth’s movements. The continuous gap between these two hands vividly illustrates the irregularity inherent in true solar time, offering a captivating and intuitive display of this celestial phenomenon.

A Louis XVI table regulator with running equation and remontoire by Robert Robin (1741-1799), 1781. Image – Christies

EoT watches and regulators crafted during this era were engineering marvels created only by the most skilled artisans in the field. For instance, Mudge’s equation of time regulator boasted a complex month-going movement comprising 18 wheels with 1,581 teeth. The largest wheel, the annual calendar wheel, featured a staggering 365 teeth. To provide context, a month-going regulator without the equation of time function typically had only eight wheels and 266 teeth in total.

Given their highly complex craftsmanship, such timepieces commanded exorbitant prices and were produced in very limited quantities. They were sought after by royalty and the wealthiest individuals, serving as precise timekeepers, prestigious status symbols, and conversation pieces. They were nothing short of mechanical marvels.

Only a select group of renowned makers crafted watches with this complexity throughout the 18th and early 19th centuries. In England, besides Mudge, other masters like George Graham and John Ellicott spearheaded this horological innovation.

Centre seconds pocket watch with running equation by Ferdinand Berthoud from circa 1756-1762. Image – The British Museum

Similarly, on the continent, notable figures such as Pierre Le Roy (1717-1785), Jean-Antoine Lépine (1720-1814), and Ferdinand Berthoud also pushed the boundaries of horological innovation.

The legacy of these master clockmakers extended beyond their contributions. Collaborations, such as those between Jean-Baptiste Lepaute and his brother Jean-André Lepaute, yielded several remarkable examples of running equation timepieces. Similarly, the intricate works of Antide Janvier (1751-1835) and Abraham Louis Breguet (1747-1823) epitomised a harmonious blend of mechanical precision and artistic finesse, setting new standards for horological excellence.

An astronomical clock by Eardley Norton (1676-1766) from 1765. Image – The Royal Collection Trust

Across the centuries, notable examples of clocks featuring running equations of time testified to the relentless pursuit of accuracy and innovation. Each timepiece, from Eardley Norton’s pioneering astronomical clock to Victor Chatriot’s (1828-1889) ornate masterpieces, represented a milestone in horological engineering.But as the 19th century dawned, the advent of mean solar time marked a pivotal shift in timekeeping practices, reflecting a broader transition towards standardised measurement systems.

19th Century Timekeeping: The Path to Global Coordination

As the 19th century unfolded, the symbiosis between timekeeping innovation and navigational necessities led to the widespread acceptance of Local Mean Time as the definitive standard for measuring time. This era distinguished itself by prioritising meantime over solar time, leveraging the concept of an imaginary sun that traverses the equator at a consistent speed. This notion was pivotal for the intricate calculations required in determining longitude, offering a degree of uniformity essential for navigation that solar time could not provide.

While not observable directly, the position of this hypothetical Sun was inferred through the consistent and predictable motion of stars around the equator, known as Sidereal Time. This celestial regularity laid a robust foundation for the computation of Mean Time, facilitating a transition that would have profound implications for timekeeping and navigation. The notable time differences between different locales highlighted the necessity for a standardised approach to time measurement, marking a significant leap toward harmonising timekeeping practices.

A sidereal and running equation of time deck watch by Stromgren og Olsen, circa 1920. Image – Antiquorum

This shift from Solar to Local meantime was not merely a technical adjustment; it represented a fundamental transformation in how time was conceptualised and utilised globally. Establishing a more consistent and universally applicable system laid the groundwork for future advancements in global time coordination. This period underscored the indispensable role of precise time measurement in the broader narrative of navigation and global exploration, setting the stage for today’s interconnected world.

Through these developments, the 19th century emerged as an essential chapter in the history of timekeeping, bridging the gap between regional timekeeping practices and the global coordination efforts that would eventually culminate in establishing standardised time zones and universal time. The legacy of this era’s timekeeping innovation continues to influence our understanding and management of time in the context of navigation and beyond, highlighting the enduring significance of these advancements in shaping our global society.

However, although this standardised measurement greatly and unequivocally simplified the structuring of daily activities, it also distanced humanity from the natural cycles that had previously dictated our existence.